Star Radiation
Temperature of a substance is related to thermal energy.
Farenheit temperature scale. Originally 100° was the temperature of a human body. 32°F is freezing. Boiling is 212°
Celcius scale. 0°C freezing, 100°C boiling
Kelvin 0K absolute zero (no energy). 273.16K ; 0.01K above the melting point of ice. Triple point of water. Water boils at 373.15K, Ice melts at 273.15K. Earth is 300K, Sun is 5800K, Center of Sun is 15,000,000K
Hot Matter Radiation
Temperature and color of light emitted is related. Hot matter radiates heat and light.

Light
Light is an electromagnetic wave
$$ c = \lambda f \tag{Eq 3.1}$$ λ = wavelength
f = frequency
c = speed of light \((3.0 * 10^8 ms^{-1})\)
Light propogates as photons ‘wave packets’. Light is quantized.
Planck’s Law of Quantisation
Energy in a photon, proportional to the frequency $$ E=hf \tag{Eq 3.2} $$ Planck’s constant h is \(6.6*10^{-34}\) J s (Planck’s law of quantisation)
Substituing 3.1: $$ E=\frac{hc}{\lambda} \tag{Eq 3.3}$$
Kinetic Energy
Average thermal energy of a particle: $$ E_{thermal} = \frac{1}{2}mv^2 = \frac{3}{2}kT \tag{Eq. 3.4}$$
k is Bolzmann constant
T is temperature
Black Body Radiation
A black body is a perfect emitter and absorber of radiation. Black Body Radiation - Wikipedia
Radiation is in thermodynamic equilibrium with matter. No flow between matter and radiation. So the body temperature describes the radiation.
Radiation is isotropic flowing in all directions. No net flow of energy.
No polarisation of the radiation.
Planck Equation
Wien approx, the left side at shorter wavelength. Rayleigh-Jeans approximation right side longer wavelengths.
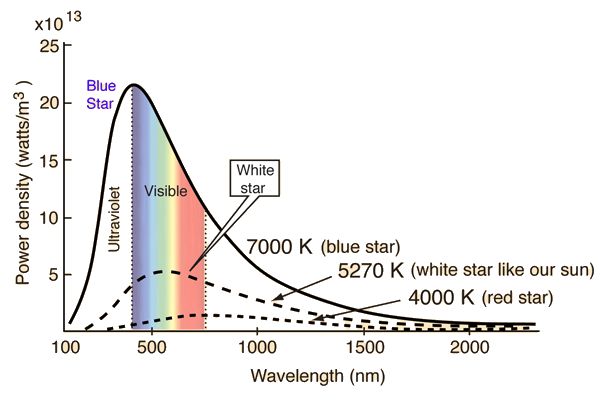
The Wien Displacement Law
Peak in the curve linked to temperature. Wien’s Law: $$ \lambda_{max}T = constant = 2.8978 * 10^{-3}mK \tag{Eq 3.5} $$
\(\lambda_{max}\) is the wavelength of max intensity radiation, T is the temperature.
Cooler objects produce radiation which peaks at longer wavelengths (redder colors), hotter objects produce radiation which peaks at shorter wavelengths (bluer colors).
Sefan-Boltzmann Law
Therefore: Flux is related to temperature. $$ F = \sigma T^4 Wm^{-2} \tag{Eq 3.6} $$ \(\sigma = 5.67*10^{-8} W m^{-2}K^{-4}\) is Stefan-Boltzmann constant
Luminosity of a star of Temperature T and Radius R: $$ L = 4 \Pi R^2 \sigma T^4 $$
Where \(4 \Pi R^2\) is the surface area of a star
For the Sun. Add Radius = \(6.96 * 10^8\), Temp = \(5800\degree K\) $$ L = 4 \Pi * (6.96 * 10^8)^2 * (5.67*10^{-8}) * 5800^4 $$ $$ L = 3.9 * 10^{26}W $$
Also for the sun, Flux:
$$ F = \frac{L_o}{4\Pi R_o^2} $$
Photometry
Filtering the wavelengths and measuring the flux near the peak of the spectrum. Known as stellar photometry.
UBV Photometric system
Three filters; U, B, V. U=360nm, B=440nm, V=550nm Ultraviolet (hard to measure through atmosphere) Blue (visual) Visible (visual) We measure apparent magnitude m_u, m_b, m_v. Shorthand UBV.
Comparing different filter measurements gives a different in magnitudes called the color index The more negative the index, the greater the ratio of short to long wavelength and the higher temperature.
(U-B) and (B-V) are color indices. U,V,B are 0 for Vega, point of reference (Vega is 10000K - main sequence A0)
U –– B —– V Wavelength
(U-B) = (B-V) = 0 : A0, 10000K
Hotter = negative Colder = positive
Kirchhoff’s Laws
1: Hot opaque body, such as black body or hot dense gas produced continuous spectrum
2: Hot transparent gas produces emission line spectrum agains a dark background
3: Cool gas in front of continuum produces absorption line spectrum. Dark lines in the spectrum are at the same place as emission spectrum for the gas.
