Stellar Magnitude
Logs Refresher
$$ \log_{10}x\text{ : Count the zeros} $$ $$ \log_{10}(100) == 2 $$ $$ 10^x = Antilog $$ $$ 10^2 = 100 $$
Stellar Magnitudes
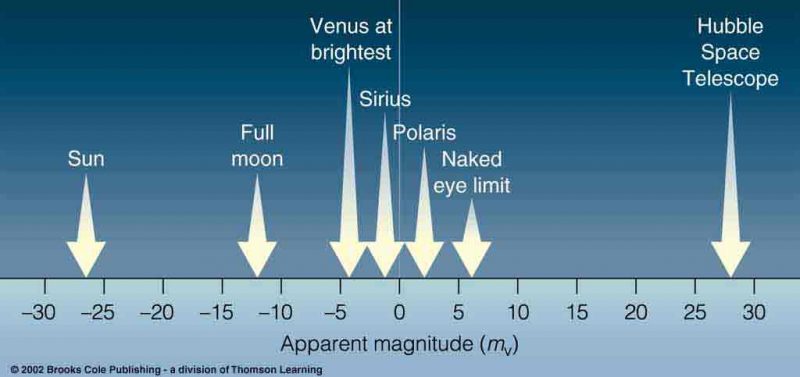
Hipparchus. The smaller the value, the brighter the object.
Sirius = \(-1.4\) (very bright)
Neptune = \(7.62\) (much less bright)
The Sun is \(-26\).
This is the ‘apparent magnitude’, how they appear. Naked eye range is 1 to 6. Best resolution of telescope we have is about 30.
Wikipedia - Apparent Magnitude
N.R. Pogson: For 2 objects, 5 magnitude difference corresponds to a factor of 100 brightness
Flux
Total flow light energy per unit area: $$ Wm^{-2} \text{ OR } Js^{-1}m^{-2} $$
Apparent mag relation (Ratio of fluxes): $$ \frac{Fm}{Fn} = 2.512^{n-m} \tag{Eq 2.1} $$ Note: Ratio = 100 == n-m of 5 (see above N.R. Pogson)
Pogson’s Relation
Difference in apparent magnitudes: $$ m - n = -2.5 * \log_{10}{\frac{Fm}{Fn}} \tag{Eq 2.2} $$ OR $$ \frac{F_m}{F_n} = 10^{-0.4*(m-n)} \tag{Eq 2.2.1}$$
$$ \text{For Eq 2.2: } 1 - 6 = 100 \tag{As expected}$$
For Flux and ratio calculation, formula can be generalized:
Zero point of apparent Mag
For a star of m = 0, and Flux Fo, apparent mag of any star is: $$ m = 2.5 \log_{10}\frac{Fm}{Fo} $$ Wikipedia - Zero Point
Luminosity
The Sun is (Solar Luminosity): $$ 4 * 10^{26} Watts $$
Inverse Square law
Astronomy Notes - Inverse Square Law
$$ \text{Surface Area Of Sphere} = 4\Pi r^2 $$
Observed Flux inversely proportional to squared distance: $$ Flux = \frac{\text{Luminosity}}{\text{Surace Area of Sphere}} $$ $$ F = \frac{L}{4\Pi d^2} \tag{Eq. 2.4} $$
Hence: $$ \frac{F_D}{F_d} = \frac{d^2}{D^2} \tag{Eq 2.5}$$ e.g. 1/3 distance ratio == 9/1 Flux ratio
Note: Gravity also has \(r^2\) falloff \(F = G\frac{m_1m_2}{r^2}\)
Absolute Magnitude
Absolute magnuitude, similar to Pogson, but with absolute Luminosity ratio $$ M - N = -2.5 * \log_{10}\frac{L_M}{L_N} $$ OR $$ \frac{L_m}{L_n} = 10^{-0.4*(M-N)} \tag{Eq 2.7.1}$$
At 10pc from star, Absolute Mag == Apparent Mag
Therefore; from Eq 2.5, a star at distance d, flux \(F_M\) at 10pc with observed flux \(F_m\) $$ \frac{F_M}{F_m} = \frac{d^2}{10^2} \tag{Eq. 2.7} $$
Combined with Eq.2.2: $$ m - M = 5 \log_{10}d - 5 \tag{Eq. 2.8} $$ (m - M) is the distance modulus
e.g. for distance 10pc: $$ m - M = 5 \log_{10}10 - 5 $$ $$ m - M = 0 $$ Therefore: at 10pc M == m
Rearranged for M: $$ M = m + 5 - 5 \log_{10}(d) $$ Link to Good Example Calculations
Stellar Colors
Worked Examples
Distance to Vega, given m = 0.03, M = 0.58
$$ 0.03 - 0.58= 5 \log_{10}d - 5 $$ $$ -0.55 = 5\log_{10}d - 5 $$ $$ 4.45 = 5 log_{10}d $$ $$ 10^{0.89} = 7.76 pcs $$ == 25 Lightyears (distance to Vega)